Je serai catégorique...

Gudule : mauvais. 1 / 10.

C'est l'histoire de deux objets qui veulent transiter par un foncteur, mais ils ne peuvent pas parce que le foncteur est plein...

Gudule : déprimant. 2 / 10.

Le seul objet qui est isomorphe à Chuck Norris, c'est Chuck Norris.

Gudule : bon, je démissionne.

Gudule ! Je sais où tu te caches ! Reviens ici tout de suite !

--------------------------------------------

Avec la théorie des ensembles de Zermelo-Fraenkel (axiome du choix ou non), la théorie des catégories est l'une des formalisations possibles des mathématiques. Donc avant d'entrer dans le vif du sujet : oui, c'est cool.

Gudule : malgré mes efforts, PJAM se délite lentement. Bientôt on va juste arriver à des chapitres dont le seul contenu sera « c'est cool ».

En fait, la théorie des catégories peut être vue comme une formalisation de très haut niveau. Vu de loin, les mathématiques s'occupent de structures qui, selon les cas, peuvent se ressembler entre elles. C'est comme ça que certaines preuves dans certains domaines différents (NDG : référence nécessaire) se trouvent en fait être similaires, parce qu'elles reposent sur des constructions qui se ressemblent. La théorie des catégories permet d'expliciter plus facilement cette « similarité ».

Une catégorie c'est :

– une classe d'objets

Gudule : attention. Une « classe », ce n'est pas un ensemble. C'est plus gros. De sorte que vous ne pouvez pas parler de l'ensemble des groupes, mais que vous pouvez parler de la « classe des groupes », c'est-à-dire, toutes les structures de groupes.

– une classe de morphismes

Gudule : à vos souhaits.

Les morphismes sont des correspondances entre objets. L'idée est que ce sont des correspondances naturelles, qui préservent la structure. Par exemple ? Un morphisme entre groupes doit préserver la structure de groupe.

On pourrait par exemple définir la catégorie des familles avec les « morphismes des familles » qui préserveraient le rôle de chaque membre de la famille. À un parent on associe un parent, à un enfant un enfant.

Gudule : cet exemple a été inventé uniquement pour employer l'expression « morphisme des familles ». Maître, arrêtez de rigoler comme un imbécile et continuez. Envoyez des exemples sérieux de catégories, par exemple.

Bah, par exemple, l'ensemble de tous les ensembles n'existe pas en théorie des ensembles, mais la « catégorie des ensembles » existe. Deux ensemble sont isomorphes s'ils ont le même nombre d'éléments (infini ou non), et les morphismes font des correspondances arbitraires entre ces éléments.

La catégorie des groupes.

La catégorie des espaces vectoriels.

La catégorie des monoïdes.

La catégorie des modules.

La catégorie des corps.

La catégorie des algèbres.

La catégorie des anneaux.

Etc.

Les catégories sont bien pour faire ce qu'on aime faire dans l'étude des structures, en algèbre : oublier les objets et s'intéresser aux structures elles-mêmes, donc à ce qui est « préservé par les morphismes ».

Vous pouvez passer d'une catégorie à l'autre en utilisant ce qu'on appelle un foncteur. Par exemple, un groupe est un ensemble. Vous pouvez « oublier » que c'est un groupe et juste le considérer comme un ensemble, passant ainsi par le « foncteur d'oubli ».

Un foncteur envoie des morphismes sur des morphismes. Si vous regardez bien, tant que vous savez comment transformer les morphismes, vous n'avez pas besoin de parler des « objets ».

(NDG : vous retrouverez cette philosophie dans un des bouquins de CN (NDA : arrête de spoiler, traître)).

Le foncteur d'oubli ne sert à peu près à rien. Plus amusant, vous pouvez parler de son foncteur adjoint, qui va « en sens inverse » : au lieu par exemple d' « oublier » la structure de groupe et de renvoyer un ensemble, il va faire le contraire, c'est-à-dire donner une structure de groupe « générale » (un groupe « libre ») à cet ensemble. Et là, c'est assez magique.

Autre exemple : la catégorie des catégories est une catégorie. Ses morphismes sont les foncteurs puisqu'ils font des correspondances entre catégories.

Gudule : gné.

Attendez, c'est pas fini. On peut faire des correspondances entre foncteurs (transformations naturelles). Ça fait des morphismes de morphismes de morphismes.

Gudule : ...

Eh, on fait de l'algèbre ou on n'en fait pas.

On fait aussi de jolis diagrammes pour représenter les morphismes. Donc ça fait de beaux dessins (celui-là est très simple, j'en cherche des meilleurs).

------------------------------

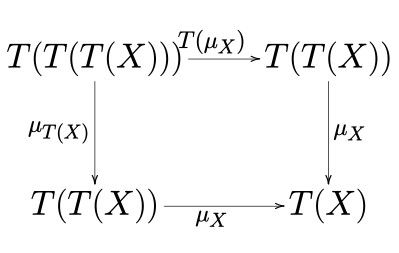
Pour une présentation en un seul bloc, sans doute plus concise que celle de Wikipédia (mais en anglais) :

http://plato.stanford.edu/entries/category-theory/