Le Présentateur : Oh regardez, à gauche, des nombres sauvages dans un champ !

L'Homme aux lunettes teintées de noir : (chuchote à son oreille) Excusez-moi, Monsieur le Présentateur, mais vous avez déjà sorti celle-là au chapitre précédent !

Le Deuxième Présentateur : (à voix haute pour capter l'attention du public et enchaîner) Et justement, ceux-ci sont des nombres de votes. Alors, pour ceux qui ne savent pas, le vote est la petite étoile sur laquelle vous pouvez ...

La Foule : On sait déjà ! On veut les résultats !

Le Deuxième Présentateur : (pour meubler) Eh oui, exactement, des résultats, des résultats que nous avons ... (cherche ses notes devant le pupitre et tourne les pages très vite) ... que nous avons ici : il s'agit toujours des données du top 1000 du classement Fantasy. Le minimum du nombre de votes est atteint à 0.

Le Matheux Rigoureux : C'est-à-dire, il existe des fictions classées et qui ont 0 votes.

Le Présentateur : Oui, oui tout à fait, et bien sûr, elles sont beaucoup plus nombreuses que les fictions qui ont 0 vues, je suppose ?

Le Deuxième Présentateur : Vous avez tout-à-fait raison, et plus précisément, 2,5% des fictions considérées, soit une sur quarante, n'ont pas de vote.

Le Présentateur : D'ailleurs, un quart des fictions totalisent moins de 21 votes. Et la moitié ont moins de 120 votes.

Le Matheux Rigoureux : Au fait, c'est ce qu'on appelle la médiane, juste comme ça. Le nombre de votes médian est donc de 120.

Le Deuxième Présentateur : (continue à lire ses notes) Trois quarts des fictions ont moins de 753 votes. Et la meilleure comporte 72 940 votes, un chiffre impressionnant.

Le Présentateur : Très impressionnant, même.

Le Matheux Rigoureux : Ces valeurs extrêmes contribuent donc à décaler la moyenne vers le haut.

Le Deuxième Présentateur : Comme pour le nombre de vues ?

Le Matheux Rigoureux : Exactement, c'est le même phénomène. Le nombre de votes moyen s'élève donc à 1 765 votes par fiction.

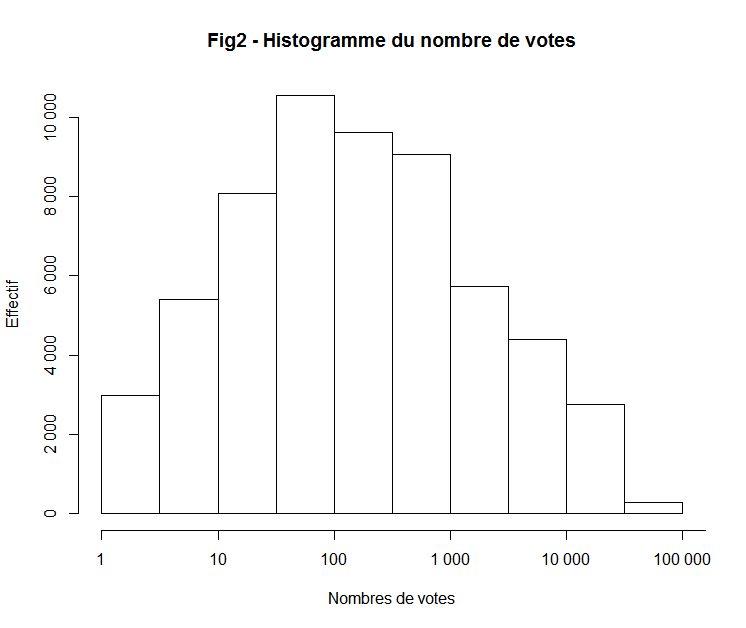
Le Présentateur : Un petit graphique ? Et d'ailleurs, on a décidé de numéroter tous les graphes, pour que ce soit plus facile d'y faire référence.

Le Présentateur : Mais non, pas celui. (À l'équipe technique) On a dit qu'on faisait la transformation en log, pour changer l'échelle, là ça va pas du tout !

Le Deuxième Présentateur : Pour rappel, on va changer l'axe horizontal, pour que ce soit plus représentatif. Ainsi au lieu de passer de 20 000 en 20 000 comme sur le précédent graphique, donc en ajoutant une quantité fixe à chaque fois, on va multiplier par 10 à chaque fois.

Le Présentateur : Le but est de pouvoir mettre sur un pied d'égalité des fictions avec des nombres de votes très différents : de 1 à plusieurs dizaines de milliers !

Mr Contrexemple : (arrive en jaillissant par un trou du plafond) Eh eh vous n'avez pas retenu ce que je vous ai dit ! L'important c'est de raisonner en termes de nombre de votes par parties !

Le Présentateur : (sereinement) J'allais y venir, justement. Patience, patience. (se tourne vers le Deuxième Présentateur) Les résultats, s'il vous plaît ?

Le Deuxième Présentateur : Eh bien les fictions qui n'ont aucun vote ont donc 0 votes par parties, ce qui est le minimum. Un quart des fictions ont moins de 2,65 votes par parties, et la moitié ont moins de 7,31 votes par parties.

Le Présentateur : Les trois quarts des fictions ont moins de 32,78 votes par parties, toujours en moyenne. Quant au record, il est tenu à 1 159 votes par parties !

Le Deuxième Présentateur : Et la moyenne s'établit à 46,75 votes par parties. Regardez ici, voici le graphique en log :

Le Présentateur : (remarque l'air de rien) Il y a des fictions qui ont moins de 0,1 votes par parties, on dirait.

Le Deuxième Présentateur : Oui, effectivement : il suffit de prendre l'exemple d'une fiction avec un seul votes et 11 parties, et ça donne un nombre moyen de 0,09 votes par parties, ce qui est plus petit que 0,1.

Le Présentateur : Alors, je pense que ça va être tout pour cette fois ?

Le Deuxième Présentateur : Tout à fait. Nous avons donc parlé de la répartition du nombre de vues et de la répartition du nombre de votes. Merci d'être toujours là, et au prochain arrêt, nous parlerons du lien entre ces deux valeurs.

Le Matheux Rigoureux : Soyez plus précis. Quel lien ? Entre quoi et quoi ?

Le Deuxième Présentateur : Entre ces deux variables aléatoires, pour employer le terme technique, que sont le nombre de vues et le nombre de votes. (Il hésite un instant) Quand on parle de variable aléatoires, ça veut dire que ce sont des nombres inconnus.

Le Matheux Rigoureux : Attention, ce ne sont pas inconnues dans le sens "nombre que l'on va chercher à calculer", comme la solution d'une équation. Ce sont des nombres inconnus parce qu'il est par définition impossible de les connaître à l'avance, comme le nombre affiché sur un dé, ou la combinaison gagnante du loto.

Le Deuxième Présentateur : Voilà, tout à fait. Et on va chercher à connaître les relations entre le le nombre de vues et le nombre de votes.

Le Présentateur : Vous pensez qu'il y a un lien ?

Le Matheux Rigoureux : Il n'y a pas de raison que les deux variables soient indépendantes, a priori.

Le Deuxième Présentateur : D'une part, oui. Et d'autre part, c'est évident qu'il ne peut pas y avoir moins de vues que de votes. Donc les vues conditionnent d'une certaine manière le nombre de votes en leur imposant une limite supérieure.

Le Matheux Rigoureux : Et inversement, le nombre de votes est forcément inférieur au nombre de vues.

Le Présentateur : Excusez-moi, c'est très intéressant, mais nous verrons ça la prochaine fois. Ce serait dommage que le train ait du retard ...

L'Avocat du Diable : (discrètement) Pour une fois qu'un train peut être à l'heure, on ne va pas s'en priver !