Le Présentateur : Oh regardez sur votre gauche, des nombres sauvages dans un champ !

Et là, d'autres nombres encore, sur votre droite ! Il y en a des milliers, et des dizaines de milliers, c'est pour ça qu'on ne peut juste pas passer des heures à les regarder tous comme ça, à les contempler ! Mais on va résumer l'information qu'ils possèdent.

Le Deuxième Présentateur : (arrive depuis un autre compartiment) Ça y est ça y est, j'ai enfin toutes les données et tous les résultats !

Le Présentateur : Mais, de quoi parlez-vous ?

Le Deuxième Présentateur : Les données sur le nombre de vues, c'est ça que vous pouvez voir autour de nous. Regardez ces rangées de nombres : pour chaque jour, pendant plusieurs mois (80j), nous avons les nombres de vues de toutes les œuvres du classement de la catégorie Fantasy. Ou presque, il y a quelques données manquantes, mais ce n'est pas bien grave.

Le Présentateur : Ah, oui, les nombres de vues ! Comment comptez-vous faire pour les étudier ?

Le Matheux Rigoureux : Ah mais désolé, je vous arrête tout de suite, mais la question est importante ! Si une fiction est souvent dans le classement, son nombre de vues apparaitra sur plusieurs jours, tandis que si une fiction passe une seule fois dans le classement, son influence sera plutôt plus faible. Votre procédure peut donc être biaisée !

Le Deuxième Présentateur : Attendez, attendez, on ne va pas tout mélanger. D'abord, la représentativité. Effectivement, sur nos données, on a plus d'informations sur les œuvres paru il y a longtemps que sur les œuvres récentes, parce qu'elles n'étaient peut-être même pas créées quand on a commencé à relever les données.

Le Matheux Rigoureux : (victorieux) Donc, il y a bien un biais !

Le Deuxième Présentateur : Oui, mais on ne peut pas y échapper. Par exemple, si une œuvre a été créée le 1er juin, on est sûr qu'elle n'apparaît pas dans le classement avant. Les analyses que nous faisons s'appliquent donc aux statistiques des fictions dans le passé, mais si la structure socio-démographique est à peu près stable, les conclusions devraient être valables également maintenant et dans le futur.

Le Matheux Rigoureux : Et pour la représentativité ? Vous n'avez relevé que les statistiques des fictions classées, que vous pouvez-vous dire sur les non-classées ?

Le Deuxième Présentateur : Alors, en fait, on ne peut rien en dire puisqu'on a pas les données (pour l'instant) ! Tout simplement. Mais si on suppose que les mêmes phénomènes s'appliquent de manière générale à toutes les fictions, on pourrait extrapoler ...

Le Présentateur : Pour l'instant, on va en rester sur ce qu'on sait, si vous voulez bien. Faites sortir les données !

Ordinateur servile : Min. : 0

Le Matheux Rigoureux : Vous voulez dire qu'il y a des œuvres qui arrivent à rentrer dans le top 1000 de Wattpad avec 0 vues ?!

Le Deuxième Présentateur : En fait, oui, ça correspond à 18 fois dans notre base, sur 80 jours, où on a des œuvres avec 0 vues dans le top 1000.

Le Présentateur : Remarquons que ça ne fait que 0.029 % de toutes les données. Pour être dans le classement, il vaut donc mieux avoir des vues ! (rires)

Le Deuxième Présentateur : (imperturbable) Et ce n'est peut-être pas un bug, il y a en a bien dans le classement, avec une vues, deux vues, trois vues. Au total, un quart des fictions considérées dans notre base de données a moins de 200 vues ! Et la moitié a moins de 1 043 vues.

Le Présentateur : Un millier de vues, c'est déjà bien respectable. D'ailleurs, en fait, les trois quarts des œuvres classées ont moins de 8 186 vues.

Ordinateur servile : Max. : 1 319 000

Le Présentateur : Certes, ça fait beaucoup de vues, ça ! Et la moyenne ?

Ordinateur servile : Moyenne : 23 170

Le Présentateur : (choqué) Pardon ? Ça veut dire que les trois quarts des fictions considérées ont un nombre beaucoup plus faible que le nombre de vues moyens ?

Le Deuxième Présentateur : (toujours imperturbable) Là, on a calculé la moyenne. Mais en fait, ce n'est pas forcément une bonne idée, parce que ce n'est pas dans ce cas une procédure très intéressante: on va faire la moyenne entre des fictions avec des centaines de vues et d'autres avec des centaines de milliers, voire des millions de vues.

Et en général, quand on a des distributions de nombres qui s'étendent directement sur plusieurs ordres de grandeur, c'est à dire on peut aller de 10 vues à 100 vues, 1 000 vues, et jusqu'à des millions de vues, la moyenne va être déformée par les valeurs extrêmes.

Le Présentateur : C'est comme, imaginez, vous comptez des billes avec votre ami dans la cour de l'école, et il y a un riche arrive avec des camions et des camions remplis de sacs de billes. LA valeur moyenne se trouve alors complètement déformée

On va donner un exemple concret plus intéressant. Mr Économiste, c'est à vous.

Mr Économiste : Merci. Hum, un des exemples les plus parlants sur les problèmes liés à la moyenne est le suivant: on a une entreprise avec 4 salariés qui gagnent chacun 1 000 € et un patron qui gagne 21 000€. Le salaire moyen est donc de 5 000€. Est-ce que ça veut dire quelque chose ?

Le Matheux Rigoureux : Ben oui c'est un nombre intermédiaire entre 1 000 et 21 000. Donc c'est logique, rassurant.

Mr Économiste : Mais d'un point de vue économique, ça ne représente rien ! Personne ne gagne 5 000€ dans cette entreprise.

Le Deuxième Présentateur : Merci beaucoup pour cet éclairage. Ici c'est pareil: on va bien pouvoir calculer le nombre de vues moyen, il y a pas de problème. Mais il ne va pas être facilement interprétable, ou plutôt ce n'est pas lui qui nous intéresse en fait. De même, les graphiques qu'on obtient vont être inutilisables, regardez par exemple :

Le Deuxième Présentateur : Mais, on va pouvoir s'en sortir en faisant ce que l'on appelle une transformation logarithmique.

Le Présentateur : Et à part ce terme barbare, ça veut dire quoi ?

Le Matheux Rigoureux : Eh bien on va comparer non pas les nombres de vues, mais les puissances de 10 associées

Le Deuxième Présentateur : Le nombre de chiffres, en fait !

Le Matheux Rigoureux : Oui en quelque sorte. Ainsi 100 vues correspondent à une puissance 2, 1 000 vues à une puissance 3, et un million de vues à une puissance 6.

Le Deuxième Présentateur : Et là, ça va être beaucoup plus pratique

Le Présentateur : Ainsi, vous êtes dans la moyenne si vous avez entre 100 et 10 000 vues ...

Mr. Contrexemple : (arrive en sautant du plafond) Non, vous vous êtes trompés ! Ce n'est pas le nombre de vues total qui est important ! C'est le nombre de vues par parties !

Le Deuxième Présentateur : ...

Le Matheux Rigoureux : Mais oui, il a raison ! Après tout, il suffirait qu'on double le nombre de parties, et hop, ça double le nombre de vues automatiquement. Ce n'est donc pas le bon critère...

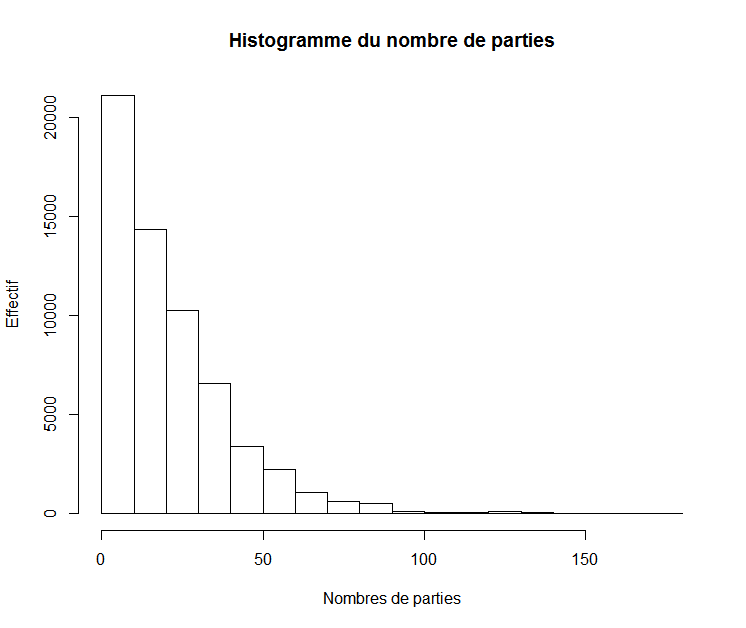
Le Présentateur : Vous avez les résultats sur le nombre de parties ?

Ordinateur servile : Min. : 1

Le Présentateur : bon c'est logique qu'il ait des histoires avec une seule partie...

Le Deuxième Présentateur : (regarde la suite des résultats) Un quart des fictions ont 7 parties ou moins, la moitié ont 17 parties ou moins, et les trois quarts ont 30 parties ou moins.

Ordinateur servile : Max. : 178

Le Présentateur : Ça fait un sacré nombre de parties, ça !

Le Deuxième Présentateur : Tout ça reste sur le même ordre de grandeur, donc la moyenne a un sens. Combien vaut-elle ?

Ordinateur servile : Moy. : 21.48 parties/fiction

Le Deuxième Présentateur : Parfait. Les connaisseurs auront remarqué que la moyenne est supérieure à la médiane (qui vaut 17), ce qui est logique compte tenu de la forme de la distribution.

Le Présentateur : Bien. Passons aux résultats sur le nombre de vues par parties. En fait, il s'agit du nombre moyen de vues par parties sur une fiction donnée.

Le Matheux Rigoureux : Plus précisément, c'est le nombre de total de vues divisé par le nombre de parties.

Mr. Contrexemple : (rire diabolique) Ahahah ! Je croyais qu'il ne fallait pas faire de moyennes sur les nombres de vues ? Vous vous êtes contredits !

Le Matheux Rigoureux : Pas vraiment. On a dit qu'il ne fallait pas faire de moyenne sur des nombres avec des ordres de grandeurs vraiment différents. Or sur une fiction donnée, on s'attend à ce qu'il y ait un lien entre le nombre de vues sur chaque partie, que ce soit environ le même ordre de grandeur.

Le Deuxième Présentateur : La procédure est donc bien justifiée. (Tape dans ses mains) Les résultats du nombre de vues par parties, si vous plait ?

Ordinateur servile : Min. : 0

Le Présentateur : C'est cohérent, ça correspond aux fictions qui ont 0 vues dont on a déjà parlé.

Le Deuxième Présentateur : Un quart des fictions ont moins de 22,20 lectures par partie, et la moitié ont moins de 61,92 lectures par partie.

Le Présentateur : Cela veut dire que l'autre moitié a plus de 61.92 lectures par partie.

Le Deuxième Présentateur : (fait mine d'être impressionné) Quelle intelligence mon cher ! Vous mériteriez un prix Nobel pour cette découverte ! Bref, les trois quarts des fictions ont moins de 362.10 vues par partie.

Ordinateur servile : Max. : 28 720 vues/partie

Le Présentateur : Ah ouais quand même ! Ça c'est de la bonne valeur extrême ! Je supose que ça doit déplacer la moyenne vers le haut ?

Ordinateur servile : Moy. : 615,80 vues/partie

Le Présentateur : (satisfait) C'est bien ce que je disais.

Le Deuxième Présentateur : Un petit graphique en log pour voir ça ?

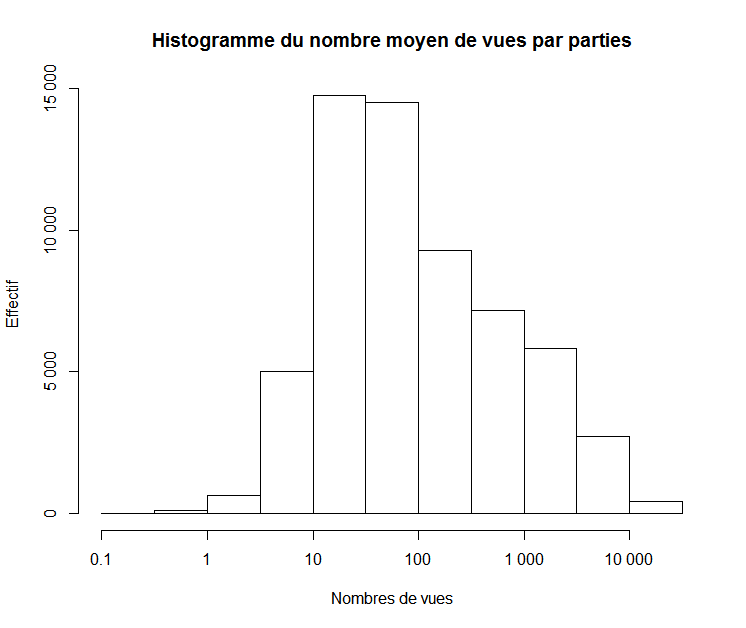
Mr. Contrexemple : Comment peut-il y avoir entre 0.1 et 1 vues , pour certaines fictions ?

Le Deuxième Présentateur : C'est parce qu'il s'agit d'un nombre moyen. Si vous avez une fiction avec 5 parties et une seule vues au total, ça vous fait 0.2 vues/partie.

Le Présentateur : Eh bien, je crois qu'on a tout vu ici, ça tombe bien, dans quelque minutes, nous arriverons au sommet de cette colline et de l'autre côté se trouve un nouveau paysage, peuplé de nombres ... Mais cette fois, ce seront des nombres de votes !

Le Deuxième Présentateur : À tout de suite !