LINEAR MODELS

Okay, welcome to my talk on linear models requested by @rosiesdiaries . A heads up for anyone reading this, this was asked for 8th grade. In the UK, that is approximately year 9 and converting it helps me to roughly gage where I'm looking at. Anyway, I hope this helps and if you need any further help with the stuff mentioned below or more linear models, just comment here or at the request section and I'll see what I can do.

Linear models are used to represent the linear relationship between two things on a graph. This is linear equation can be written in the form y = mx + c.

Why don't we look more at this equation:
- y is the y co-ordinate on the graph
- m is the gradient of the graph (how many you go up every 1 you go across) 
- x is the x co-ordinate on the graph
- c is where the line crosses the y axis (y intercept)

Gradients are the number you go up or down by every 1 you go across. For instance, going from (1,1) to (2,2) would be a gradient of 1 and going from (1,1) to (2,3) would be a gradient of 2. Although going from (1,3) to (2,1) would mean you're going down 2 when you go across by 1 so gradient is -2.  But, if your slope doesn't even reach 1 point higher of lower after going 1 across, then you will have a fractional gradient and will have to take a larger selection of points.

The gradient is also known as: the change in y/change in x (/ = divided)

For example:

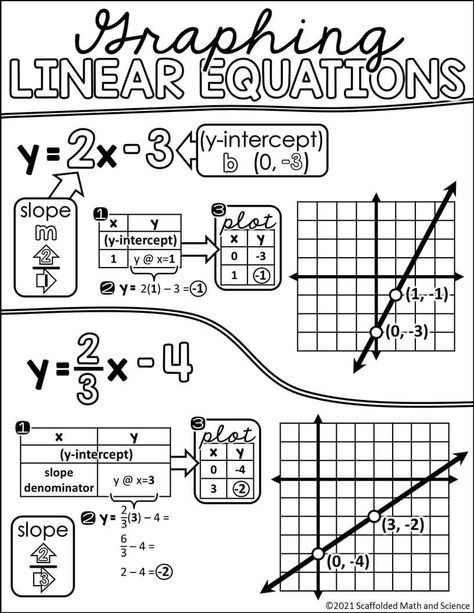
(found on pinterest) 

Here we have two examples of linear models. In the first one, we can see that the line went from (0,-3) to (1, -1) so even though it went across one, it went up 2 which gives it the gradient 2. So far, you have the equation: y = 2x + c

And even if you didn't have the line drawn on the graph, you could find the y intercept by subbing (0,-3) into what you've already found which gives you -3 = 2(0) + c.

As 2 x 0 = 0 it means c = -3 as shown above.

The same can also be done for the example beneath. 

TIY 1 & 2 (answers at bottom of page):

NOTE: Slope is same as gradient

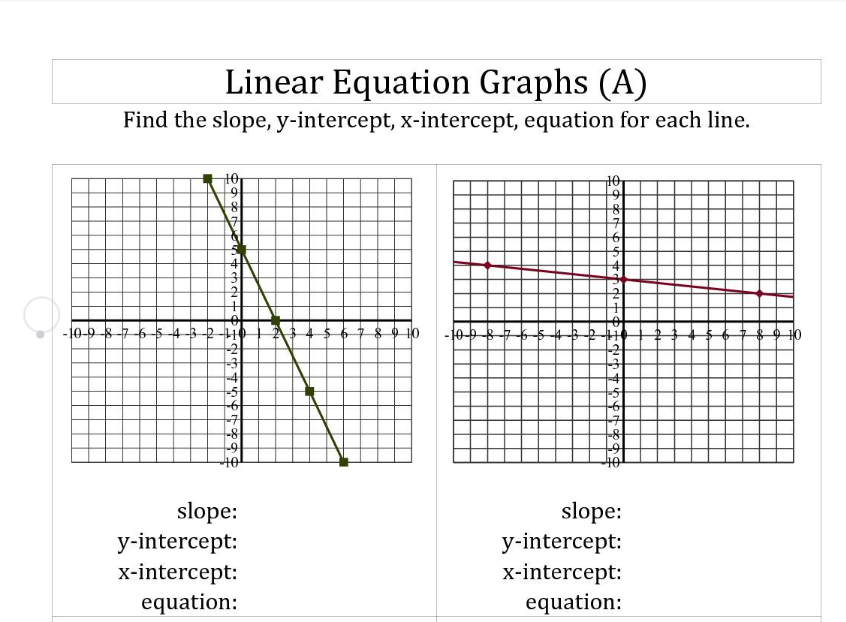
( found on askworksheet.com)

Also, you can have multiple lines on a single graph which are systems of equations. 

Now to find the equations of these lines is the same as before. But you may be asked to find the solution of the system (the two lines). Although you may spot the solution graphically, you will have to show your workings so the best way is to look at the equations of the lines. 

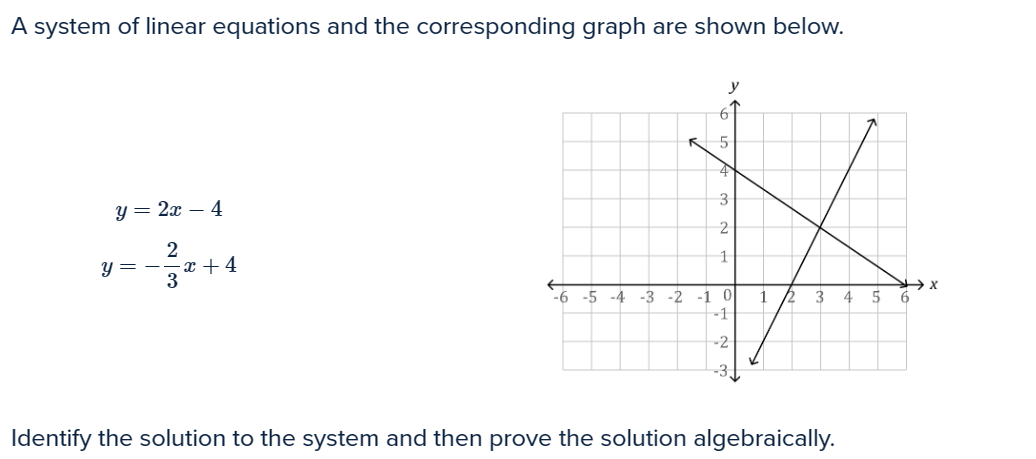
(found on fishtanklearning.org)

as you can see there are two equations: 
y = 2x -4
y = -2/3 x +4

Now, the easiest thing to do is to set the equations equal to each other and we can do this as they both equal y (if you are given equations that aren't, ALWAYS rearrange to make y the subject). 

Therefore:

2x - 4 = -2/3 x + 4 

And from there, it's just solving:

Add 4 to both sides: 2x = -2/3 x + 8
Add 2/3 x to both sides: 8/3 x = 8 
Divide both sides by 8: 1/3 x = 1
Multiply both sides by 3: x = 3

Now you have the x solution where the lines meet, you sub it into any equation, it doesn't matter which, to find the y:

y = 2(3) - 4
y = 6 - 4
y = 2

Therefore, the solution of these equations is (3,2) and we can see on the graph that it's correct!

TIY 3:

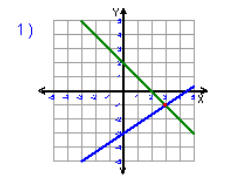
(found on studyingworksheets.com) 

find equation of green line:
find equation of blue line:
find solution of system:

I hope this helps! If you would like any further questions to try or you don't quite get it yet, please don't be afraid to ask.

Class dismissed!

Math meme time:
There will always be a math meme at the end, just a heads up. Let's make maths more fun!

TIY answers:

1: slope = -2.5
y intercept = 5
x intercept = 2
equation: y = -2.5x + 5

2: slope = -1/8
y intercept = 3 
x intercept = 24
equation: y = -1/8 x + 3

3: green line: y = -x + 2
blue line: y = 2/3 x - 3
solution: (3, -1)