« Science, frontière de l'infini, vers laquelle voyage notre chercheur. Sa mission : explorer de nouveaux mondes étranges, découvrir de nouveaux théorèmes, d'autres théories et au mépris du danger, affronter des armées d'étudiants mal embouchés. »

Gudule, tu t'es trompé de bande-annonce, celle-là c'est pour quand je serai grand.

Gudule : désolé.

« Nous reprenons PJAM en douceur, les prochains segments sont censés parler un peu de graphes. Ici rien ne devrait faire peur. Après tout, les graphes, c'est simple, comme objet, n'est-ce pas ? Oh, attendez, une image me revient à l'esprit. »

CN : bon, on a mis ça, on peut commencer.

Il essuie les postillons du meme, se frotte les mains, et finit d'engloutir un yaourt aux fruits.

CN : Gudule, pourquoi ce yaourt m'a-t-il supplié de l'épargner en français ? Nous sommes revenus en France, c'est ça ?

Gudule acquiesce silencieusement (tout en cherchant frénétiquement dans le dictionnaire l'orthographe du mot « acquiesce »). Le rideau lui tombe dessus tandis que CN branche la 6e symphonie de Mahler sur un vieux phonographe crachotant.

---------------------------

Parlons donc des nombres de Ramsey, et plus généralement, de la théorie de Ramsey.

Frank Ramsey est un mathématicien né en 1903 et mort en 1930, ce qui signifie qu'en à peine quelques années d'activité, il a réussi à mettre son nom dans les annales des mathématiques. Encore une fois, inclinons-nous devant un homme illustre qui a quitté trop tôt le monde des sciences.

Gudule : comme tout est en crescendo dans ce recueil, nous parlerons plus tard de Galois.

Au cours de quelques lectures, j'avais vu passer le nom « Ramsey » et rapidement oublié celui-ci. Puis je suis retombé sérieusement sur la théorie de Ramsey et j'ai beaucoup aimé. En voici le principe de base.

Théorie de Ramsey (Gudule) : le désordre complet n'existe pas. (Phrase souvent attribuée à Theodore Motzkin, un autre matheux).

Imaginez que vous étudiez des objets mathématiques, disons des structures finies (je ne m'appesantis pas sur la définition exacte de structure, ses tenants, ses aboutissants et les stations intermédiaires. Des objets, quoi). L'objet de la théorie de Ramsey est de trouver, dans des structures qui peuvent donc être de n'importe quelle forme, des motifs réguliers. À coup sûr. Pas question de probabilisto-mochetés, ici c'est prouvé et vrai. Bien sûr, le meilleur exemple est donné par le théorème de Ramsey lui-même, et il parle de graphes.

Un graphe est un ensemble de trucs (sommets) reliés par des arêtes (sans notion de direction, contrairement par exemple aux liens d'abonnements dans Wappy : lorsque je suis abonné à whitevador, whitevador n'est pas forcément abonné à moi (mais le sera bientôt car il aura découvert mon incroyable génie).

Gudule : les vacances, c'est bon pour le moral.

Vous pouvez modéliser beaucoup de systèmes provenant du monde réel avec des graphes. Comme nous sommes en maths, tout ceci n'a pas d'importance. Un graphe est un graphe, et c'est tout.

Une version faible du théorème de Ramsey dit ceci :

Théorème (Ramsey, version Gudule) : considérez un entier k. Dans un graphe quelconque, du moment qu'il est assez gros, vous pouvez trouver soit : k sommets qui sont tous reliés entre eux (un graphe complet), soit k sommets dont aucun n'est relié aux autres (le complémentaire d'un graphe complet, pour dire ça simplement).

Le pire, c'est que la démonstration de ce théorème n'est pas très difficile. Et même sa version complète.

Théorème (Ramsey) : considérez c couleurs (c est un entier). Considérez des entiers n1, ... nc. Il existe alors un nombre, noté R(n1 ... nc) tel que : en prenant un graphe à R(n1 ... nc) sommets, complet (donc des arêtes entre chaque paire de sommets) et où les arêtes sont coloriées comme vous voulez avec les c couleurs, il contient : soit n1 sommets tous reliés avec la couleur 1, soit n2 sommets tous reliés avec la couleur 2... soit nc tous reliés avec la couleur c.

Avouez que non seulement, c'est impressionnant du point de vue de l'ordre (si votre graphe est assez gros, il y a des sous-graphes avec une seule couleur), et en plus vous avez une maîtrise assez bonne de ces sous-structures. Eh bien ça aussi, c'est étonnamment facile à démontrer.

Souvenez-vous quand vous étiez petits : vous construisiez en légos en mélangeant les couleurs (sacrilège, mais enfin ! vous étiez jeunes). Eh bien, s'il y avait suffisamment de dimensions dans l'espace et si vous construisiez des objets compacts avec assez de pièces de légos, vous finiriez par y retrouver des sous-assemblages de la même couleur, aussi grands que vous voulez.

Gudule : on peut donc dire que les graphes ne sont pas si difficiles que ça.

C'était un piège, Gudule. Il y a des problèmes ouverts très, très difficiles dans ce domaine. Les graphes nous ont encore eus.

https://youtu.be/4F4qzPbcFiA

Gudule : avouez que nous n'avions pas besoin de cette vidéo.

En effet, le théorème de Ramsey (et ça se voit très bien sur la démonstration) dit « il existe un nombre tel que... » etc. Nombre que l'on nomme « nombre de Ramsey » avec un beau R.  Donc par exemple, R(3, 3) est le nombre de sommets à partir duquel tout graphe (non colorié) contient soit un triangle (trois sommets reliés entre eux, ça fait bien un triangle), soit le complémentaire d'un triangle (trois sommets qui ne sont pas reliés entre eux). Et il vaut 6.

Gudule : plus d'infos sur Wikipédia, une source d'informations qu'on ne présente plus (des fois en maths c'est un peu technique, hélas).

Donc on prouve que ce nombre existe, mais on ne le calcule pas. Là est le problème. En fait, on n'a pas vraiment de moyen de le calculer, autre que :

– le borner comme on peut, comme quand vous étiez jeune et vous jouiez à « plus ou moins » : c'est plus grand que tant, c'est plus petit que tant.

– terminer en testant toutes les possibilités.

Alors, tester toutes les possibilités quand on a des graphes à 6 sommets, ça va. Mais les nombres de Ramsey ont une fâcheuse tendance à grandir. Ils deviennent très, très grands. Imaginez que ce soit de l'ordre de 1000 (et encore, 1000 en maths ce n'est pas bien grand comme nombre). Vous voulez tester tous les graphes à 1000 sommets pour voir si ça marche ou pas ? Mais allez-y, mon brave. Ça vous donne un nombre de structures astronomique : (deux puissance 499500) (divisé par 1000!, la factorielle de 1000, pour ajouter aux détails sordides).

Gudule : ça fait très beaucoup.

Bien sûr, on peut réduire le champ des recherches, avec un peu d'huile de coude et de suc de neurones. Il n'empêche que R(5,5) n'est pas connu, par exemple, alors qu'il est entre 43 et 49.

On ne sait donc pas où exactement, entre 43 et 49 sommets, apparaît dans un graphe quelconque un graphe complet à cinq sommets ou son complémentaire (un graphe vide à cinq sommets).

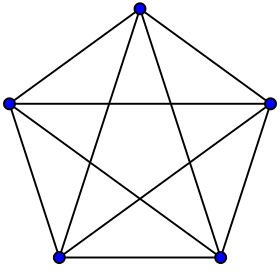
Qui dit cinq sommets dit pentacle, et c'est sur ce problème tout satanique que je vous laisse méditer.

------------------

Je mentionne whitevador pour son livre sur le Big Data. Il a à peine commencé que j'y flaire le doux parfum des maths. Alors, ça parle plutôt de statistiques et de probas, donc ce n'est pas censé être ma tasse de thé... et pourtant je vous encourage quand même à le suivre !

À mes débuts, je me suis porté en quête de maths sur Wappy et je n'en avais pas trouvé (c'est aussi pour ça que j'en sème un peu). Avec cette phrase, "Voyage au pays du Big Data" est définitivement entré dans cette catégorie que je cherchais : « Oh regardez sur votre gauche, des nombres sauvages dans un champ ! »

Tout est dit.