Il y a plein de raisons d'aimer les L-systèmes (ou systèmes de Lindenmayer). Gudule en fait même la publicité.

Gudule : grâce aux L-systèmes, ma vie est devenue merveilleuse. Avant les L-systèmes, quand je dessinais un arbre j'obtenais ça :

avec les L-systèmes, j'obtiens ça :

FTM : pour les besoins de l'expérience, nous avons transformé Gudule en tortue.

Gudule : pour ma plus grande joie.

Un L-système est juste un système de réécriture qui produit des mots. Vous disposez d'un alphabet, par exemple F, +, -, et vous produisez des « mots » (des suites de lettres) en :

– partant d'un état initial (mettons F)

– à chaque « nouvelle étape », remplaçant dans le mot précédent les symboles selon certaines règles (mettons : F → F+F-FF)

Par exemple, si votre état initial est F et que la seule règle est F → F+F-FF, alors vous avez :

– étape 0 : F

– étape 1 : F+F-FF

– étape 2 : F+F-FF+F+F-FF-F+F-FFF+F-FF

etc. Ça devient assez rapidement moche.

Gudule : je suis très désappointé d'avoir été transformé en tortue. Une justification serait la bienvenue, maître.

Lindenmayer (1925-1989) était un biologiste et il a inventé les L-systèmes pour modéliser la croissance des plantes. Comment croît une plante ? Vous partez d'un petit bout végétal, et vous remplacez certains morceaux par des motifs, selon certaines règles. Le bourgeon devient une branche sur laquelle vous avez d'autres bourgeons, etc.

Gudule : c'est l'idée, mais si un botaniste passe par ici, je pense qu'il se rendra compte que vous mélangez tout.

Et cette idée de remplacements successifs par des motifs de plus en plus complexes, Gudule ?

Gudule : fractales, bien sûr. Mais on parle toujours de « mots », là.

Un L-système est plutôt fait pour générer des figures géométriques, en utilisant la « Turtle Syntax ». L'idée remonte à loin : vous faites un tracé à l'aide d'une petite tortue. Vous pouvez :

– faire avancer la tortue

– faire tourner la tortue

Gudule : j'ai peur de comprendre pourquoi vous m'avez scotché un crayon sur la carapace.

Pour générer de superbes arbres fractals à l'aide d'un L-système, vous faites générer par ce dernier une instruction en Turtle Syntax. F+F-FF+-... etc.

Dans cette syntaxe, F veut dire « avance, sale bête », + veut dire « tourne à droite de d degrés », - veut dire « tourne à gauche ». Vous voyez le tableau.

Donc ça se programme étonnamment bien.

Gudule : et malgré ça, vous avez copié la moitié du code sur Internet.

Dessine plutôt, Gudule la tortue.

Gudule : Mais je suis une tortue. Je suis leeeeeent ! C'est absurde.

Lorsque l'art, l'informatique et les mathématiques se rejoignent, le larbin (même syndicalisé) se tait.

Il est possible, par exemple, de tracer la courbe du dragon (une fractale bien connue), à l'aide d'un L-système dont voici la formule :

– départ : FX

– réécritures : X → X+YF+, Y → -FX-Y

L'angle de rotation de la tortue est 90 degrés. X et Y sont des symboles sans instruction, juste là pour faire fonctionner le L-système, pas la tortue.

Vas-y, Gudule.

Gudule : gné.

Vous devinez que ce genre de construction est un don du FTM pour les créateurs de modèles 3D « réalistes » de plantes, par exemple. Parce que oui, on peut aussi faire ça en 3D. Et l'industrie du jeu vidéo raffole de 3D, paraît-il.

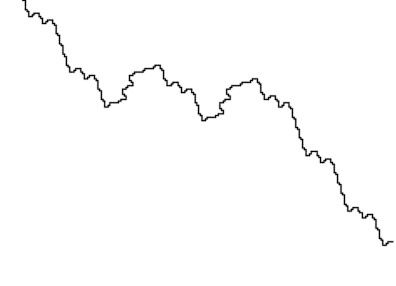
Pendant ce temps, je m'amuse avec un tracé de côte fractal (avec la règle F → FF-F+F-F+FFF et en partant de F). Allez, plus vite, Gudule.

Gudule : arf.

Quant aux L-systèmes en eux même, il s'agit ni plus ni moins que d'un exemple historique, utile et sympathique de grammaire formelle, c'est-à-dire un système de réécriture qu'on peut prendre de manière un peu plus générale. Par exemple, les grammaires hors-contexte sont définies par un ensemble de règles de production qui remplacent certains symboles particuliers par des motifs de symboles. Cette façon de décrire un langage (l'ensemble des mots produits par la grammaire) est fort sympathique. C'est comme ça qu'on va abstraire la syntaxe d'un langage de programmation, par exemple...

Gudule : mais CN va s'arrêter là parce qu'il n'a pas étudié les compilateurs dans sa vie.

Moui. Je suis juste tombé par hasard sur les grammaires hors-contexte pour des applications un peu plus ésotériques (certains problèmes de calculabilité).

Gudule : votre vie scientifique est loin d'être trépidante, maître. On ne va pas la mentionner dans ces pages. Et retransformez-moi, SVP.

------------------------------------------------------

Un petit chapitre apparu vraiment par hasard... parce que c'est marrant, c'est joli, et c'est encore des fractales.

Il a sans doute une tête de TP d'info.

Merci pour vos lectures et vos commentaires :)