L'hypothèse de Riemann date de 1859. C'était donc déjà un vieux problème à l'époque où Hilbert en en fait l'un de ses 23 problèmes de 1900.

Oui, non content de porter un étrange chapeau sur la moitié des photos que vous trouverez de lui sur Internet, Hilbert est vraiment partout, dans le monde des maths, et dans ce bouquin.

Gudule : pensez-y. Dans un siècle, la seule photo qu'il restera de vous sera celle sur laquelle, une bouteille de bière bon marché à la main, une paire d'oreilles de Mickey sur la tête, vous dansez la java en chemise à fleurs hawaïenne sur un tractopelle tout en gobant un yaourt.

--------------------------------

Fondation Gudule pour l'oubli numérique.

Évitez à vos descendants et aux archéologues du futur de tomber sur des choses pareilles. Agissons ensemble pour les protéger. Faites un don.

---------------------------------

Fondation Alcibiade contre le gobage de yaourts.

Parce que les produits laitiers ont eux aussi un cœur, faites un don.

----------------------------------

Gudule : malgré toutes les pubs, je manque encore de financement pour mon projet de chronique. Il ne me reste plus qu'à fonder une secte.

Rejoignez les adorateurs du Flying Tortellini Monster !

Le créateur de l'univers nous est apparu, porteur d'un message de paix et de tolérance. Dans notre monde troublé, perclus par la consommation outrancière, il est plus que jamais essentiel d'apprendre à relativiser l'importance que nous accordons à nos possessions matérielles. Parce qu'elles ne vous sont pas essentielles, mais qu'elles sont précieuses pour permettre de répandre le message du FTM, faites un don.

---------------------------

Dans la catégorie des problèmes du millénaire, l'hypothèse de Riemann est moins élémentaire que la conjecture de Godlbach, par exemple, car on a besoin d'objets plus compliqués pour l'énoncer. Mais elle reste assez « simple » dans ce cadre. Plus simple que la conjecture de Poincaré ou la conjecture BSD.

Gudule : il faut savoir que CN adore la conjecture BSD, mais qu'elle est délicate à présenter. Depuis environ un mois, il y réfléchit et n'en dort plus.

Plutôt que de parler tout seul, Gudule, ramène-moi un cinquième café s'il te plaît. Merci.

L'hypothèse de Riemann relie deux choses à première vue séparées :

– l'analyse complexe

– la théorie des nombres

La théorie des nombres, c'est ce qu'on a vu avec la comète de Goldbach : étudier les propriétés des nombres entiers, et de certaines extensions sur lesquelles je ne veux pas m'appesantir (LibreOffice, tu es sûr de l'orthographe de ce mot ?). Les nombres premiers, comme nous l'avons déjà vu, en sont les stars.

L'analyse complexe s'intéresse à des fonctions d'une variable complexe, c'est-à-dire des gens qui :

– mangent des nombres complexes

– renvoient d'autres nombres complexes

Où un « nombre complexe » est toujours quelqu'un qui s'écrit a + bi, autrement dit un nombre à « deux coordonnées » réelles.

La fonction Zêta de Riemann est de ces gens-là. Il s'agit du prototype le plus simple des « fonctions Zêta » qu'on trouve en fait partout en géométrie algébrique, en théorie des nombres, etc. Pourtant, la fonction Zêta est encore mal connue, comme en témoigne l'hypothèse de Riemann.

La définition de la fonction Zêta, Gudule.

Gudule : Zêta(s) est : la somme, infinie, de tous les entiers mis à la puissance (-s). J'appelle pas ça simple, maître.

Par exemple, zêta(-1) = 1 + 2 + 3 + ...  : la somme infinie des entiers (mis à la puissance 1).

Gudule : mon FTM, je sens que le pauvre homme ne s'est pas remis de son coup de batte. Il veut additionner tous les entiers. C'est ridicule.

À la base, avec cette définition, Zêta n'est pas définie pour tous les s, évidemment. D'ailleurs, définir précisément ce que veut dire « puissance s » pour un nombre s non entier (et même complexe, hem) me porterait un peu loin pour l'instant et je vais supposer que c'est bon tant que « s n'est pas trop gros ». Ce qui est important, c'est qu'on peut montrer qu'il existe une manière unique de prolonger la fonction de façon à définir « Zêta » pour tous les complexes.

Gudule : sauf 1.

Sauf 1, parce qu'en approchant de 1, on se crashe à tous les coups.

Voici maintenant le tracé de cette fonction (obtenu en 3 lignes en Python grâce à matplotlib et mpmath). C'est très psychédélique, parce qu'on représente une fonction à valeurs complexes, donc à deux coordonnées : en un point donné (a,b), la luminosité et la couleur contiennent respectivement les deux « informations » issues du nombre complexe a + bi : sa « taille » (module) et sa « direction » (argument).

Gudule : jusque-là, ça fait juste mal aux yeux. Mais les lecteurs sont habitués, ils en ont vu d'autres.

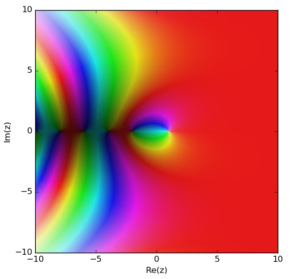
L'hypothèse de Riemann s'intéresse aux points en lesquels Zêta s'annule. Cette conjecture est que tous les points où la fonction s'annule (les zéros) qui sont situés sur la moitié droite du plan sont sur une droite verticale x = 1/2. Donc ont tous la même coordonnée x = 1/2, ou bien encore la même partie réelle 1/2 si vous les voyez comme des nombres complexes.

Pour infirmer cette hypothèse, il suffit de trouver un zéro qui ne marche pas.

Gudule : et évidemment, on n'en a pas trouvé.

Ma foi, en 2004 on en était à 10 000 milliards, et ils étaient encore tous sur la droite. Ça donne envie de dire que l'hypothèse est vraie, et en même temps, peut-être que loin, très loin dans des régions inexplorées, il y a un zéro qui trolle.

L'hypothèse de Riemann est en fait reliée à la répartition des nombres premiers. Si l'hypothèse est vraie, elle montre que malgré leur tendance à se mettre n'importe où, il y a une certaine « régularité » dans la disposition des nombres premiers.

Gudule : la phrase devenant floue, vous devinez qu'on arrive aux limites du savoir de CN.

L'important, c'est qu'on ne sait pas. Si on a un jour la réponse, ce sera un grand jour (le gagnant empochera un million de dollars, offert par le Clay Mathematics Institute, mais cet d'argent n'a aucune importance face à la célébrité qu'il gagnera au sein de la communauté mathématique), mais ça ne va pas beaucoup changer en pratique. Aujourd'hui, de nombreux résultats sont prouvés « sous réserve que l'hypothèse de Riemann est vraie ». Par exemple, certains algorithmes sur des entiers (décomposition en nombres premiers, etc.) sont « vrais » en supposant l'hypothèse vraie. Et ils marchent très bien comme ça.

Gudule : je ne vous savais pas aussi préoccupé par la « pratique », maître.

Excuse-moi, c'est mon côté « informatique » qui ressort un peu. Après tout, la théorie des nombres, c'est tellement orienté vers des applications pratiques...

------------------------------

Encore un chapitre ! J'ai arrêté de compter, il faudrait peut-être que je le fasse.

PJAM devient aussi bordélique sur Wattpad, que sur mon ordinateur, que dans mon propre crâne.

J'espère que tout ça vous plaît, chers lecteurs, et à ce stade je suis ouvert à toutes propositions de futurs sujets à traiter.

À venir sans doute : les nombres (réels, complexes, quaternions, algébriques, transcendants... ), le théorème de Fermat-Wiles et la géométrie algébrique... et un jour, la conjecture de Birch-Swinnerton-Dyer (BSD).