Quand vous étiez petits, il y avait forcément une carte du monde accrochée dans votre salle de classe, ou quelque chose dans le genre (un vitrail glauque, un tableau, n'importe quelle image avec des aplats de couleur bien séparés suffit). La carte du monde est au cours de géographie ce que le tableau périodique des éléments est au cours de physique-chimie : ce qui attire votre regard avec insistance quand vous commencez à vous ennuyer. Si vous vous ennuyez vraiment beaucoup, vous finissez par apprendre par cœur le nom de tous les éléments du tableau (respectivement, les noms de tous les pays). Ou vous apprenez au moins qu'il en existe un qui s'appelle le Technétium et que c'est le plus léger dont il n'existe aucun isotope non radioactif, respectivement, que Thimphou est la capitale du Bhoutan.

Si vous regardez fixement la carte trop longtemps, vous finissez bien sûr par devenir fou.

Gudule : il a tenté l'expérience. Et j'ai commencé à lui apparaître en rêve. Tout est lié.

Donc ne faites pas ça. En revanche, en regardant une carte on peut finir par se poser la question fondamentale : de combien de couleurs a-t-on besoin pour colorier ?

Gudule : faut-il être déjà fou pour se poser cette question ? Le débat est lancé.

Prenez une carte avec 200 pays. 200 couleurs suffiront, mais c'est un peu beaucoup. Tout ce qu'on veut, c'est bien sûr que deux pays limitrophes n'aient pas la même couleur.

Avec combien de couleurs puis-je colorier n'importe quelle carte ?

(Le FTM surgit, entouré d'éclairs et de fumigènes bon marché empruntés à Michael Bay)

FTM : la réponse est 42 !

La réponse est 4. C'est le « théorème des 4 couleurs ».

FTM : oh, je me suis encore trompé de question, excusez-moi.

(Vexé, le FTM repart dans un espace interdimensionnel.)

C'est une conjecture très vieille (XIXe siècle) qui a été annoncée comme « démontrée » depuis les années 70. Mais elle a donné lieu à des débats quant à la notion de « démonstration ». En fait, la démonstration repose sur l'usage de l'ordinateur, ce qui est plutôt une première. Après un peu de travail à la main, il faut analyser dans les 1500 cas différents.

Depuis 2005, on dispose d'une démonstration complète en Coq. Coq est un assistant de preuve développé par des labos de recherche français (vous le devinez au nom, bande de petits malins). Concrètement, il manipule un langage formel dans lequel vous pouvez exprimer des preuves mathématiques de façon parfaitement rigoureuse et les vérifier de manière automatique.

NON, il ne prouve pas à votre place, personne ne fait ça (cf. le Entscheidungsproblem). En revanche, il valide votre preuve. Ce qui est pratique dans un cas comme le théorème en question, trop long pour être vérifié à la main par un être sain d'esprit.

(Seul hic potentiel : comme Coq n'est pas un mathématicien, vous vous reposez bien sûr sur la supposition qu'il ne comporte pas d'erreur. Autant vous le dire tout de suite, j'ai plus confiance en ce logiciel qu'en n'importe quel être humain, faillibles que nous sommes.)

Je suis personnellement un fan de Coq, mais conscient comme tout le monde que la preuve « formelle » ne remplacera jamais la démonstration à la main, faite par un humain, avec des mots. Parce que traduire une preuve dans le langage de Coq, fût-il parfaitement conforme à la logique, est une calamité. Paradoxalement, Coq est utile pour vérifier de très longues et très absconses preuves, mais il génère ce faisant une quantité de travail de « traduction » astronomique.

Illustrons le théorème des 4 couleurs avec un exemple. Gudule, trouve-moi une carte avec pas trop de pays.

Gudule : voilà.

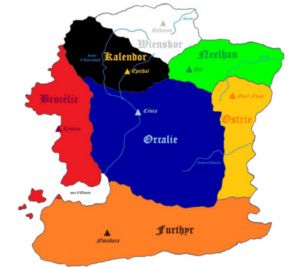
Bien. Diantre. 7 couleurs au total, pour 7 pays, c'est trop pour moi. Gudule, recoloriage.

Gudule : voilà le travail.

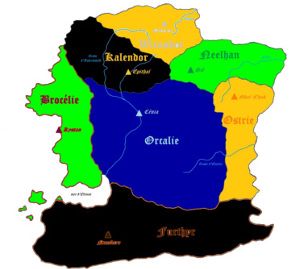
(Je donne à Gudule des choses faciles à faire pour qu'il prenne confiance en lui, tout ça. Quand on a un larbin, il faut aussi l'encourager)

Gudule : maître, qu'est-ce que vous racontiez dans cette parenthèse ?

Ahem.

Je vous assure que ça marche quelle que soit l'intrication des pays que vous pouvez imaginer. Si vous n'êtes pas convaincus, n'hésitez pas à tester. Prenez vos crayons de couleurs, hurlez hystériquement, lancez-vous.

Comment démontre-t-on le théorème ? Hem, c'est compliqué. Mais la chose vraiment importante est que ce n'est pas un théorème sur les cartes. Une carte n'est pas un objet mathématique. On parle en fait ici de graphes.

Définition (Gudule) : un graphe, ce sont des points (sommets) reliés entre eux par des arêtes.

Les graphes sont un type de structure extrêmement simple et aux propriétés pourtant extrêmement subtiles, comme en témoigne le théorème des 4 couleurs... et un paquet d'autres résultats à s'arracher les cheveux. La structure des graphes, les graphes aléatoires, les algorithmes de graphes... tout ça représente des pans entiers de la recherche mathématique. Les applications sont immenses, parce que nombreuses sont les données issues du monde réel se représentant facilement comme un graphe.

Par exemple ? Wattpad est un graphe, si vous le considérez comme un paquet de gens reliés entre eux par des abonnements.

Et une carte est un graphe, si vous considérez les pays comme les sommets, reliés entre eux quand ils sont limitrophes. Exemple avec notre carte.

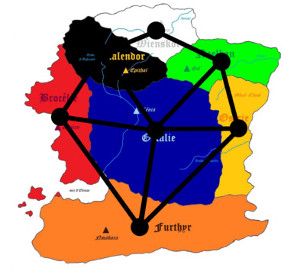
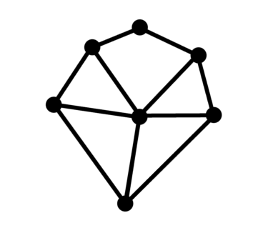
La question pour les graphes est : puis-je colorier tel ou tel graphe avec tel ou tel nombre de couleurs, de façon à ce que deux sommets limitrophes (adjacents) n'aient pas la même couleur ? Bien sûr, pour les graphes en général, c'est une question stupide. Vous avez le droit de relier tous les sommets comme vous l'entendez, donc il faudrait autant de couleurs que de sommets.

Mais une carte n'est pas n'importe quel graphe. C'est un graphe planaire, ce qui signifie que vous pouvez le tracer sur une feuille sans que deux arêtes se croisent.

Théorème des 4 couleurs (version pour les grands) : tout graphe planaire peut être colorié avec 4 couleurs.

J'ai envie de dire que l'étude de ce genre de graphes est un sujet en soi... mais c'est le cas pour l'étude de n'importe quoi dans les graphes. Un petit monde qui paraît tellement gentil et simple à première vue, alors que le FTM s'y est donné à cœur joie pour les problèmes affreux, les théorèmes difficiles aux démonstrations effrayantes et les résultats contre-intuitifs.

À chaque fois que je lis un article parlant de graphes, c'est une claque. Il peut exister des algorithmes ingénieux, mais qui nécessitent 30 pages d'explications. Il peut exister des théorèmes dont la démonstration s'étale sur des centaines de pages. En bref, vous avez l'impression que c'est un bac à sable, mais en réalité, c'est un concentré de maths.

Voilà pourquoi j'adore les graphes (et j'en ai peur).

------------------------

Merci à @JBSchrottenloher pour le prêt de la carte, héhé. J'avais la flemme d'en inventer une moi-même. Et de reprendre les régions françaises ; Gudule a trouvé qu'il y en avait trop et que c'était long à colorier.

Gudule : PJAM vient d'être nominé comme le bouquin de maths avec les illustrations les plus moches de tous les temps. Maître ! Envoyons les fractales !! Les fractaaaaales !!

Ça ne saurait tarder.