Vectores

Un vector es un elemento que contiene un par ordenado de números

ā = {2 ; 4}

Dónde en el plano cartesiano si:
y = 4
entonces:
x = 2

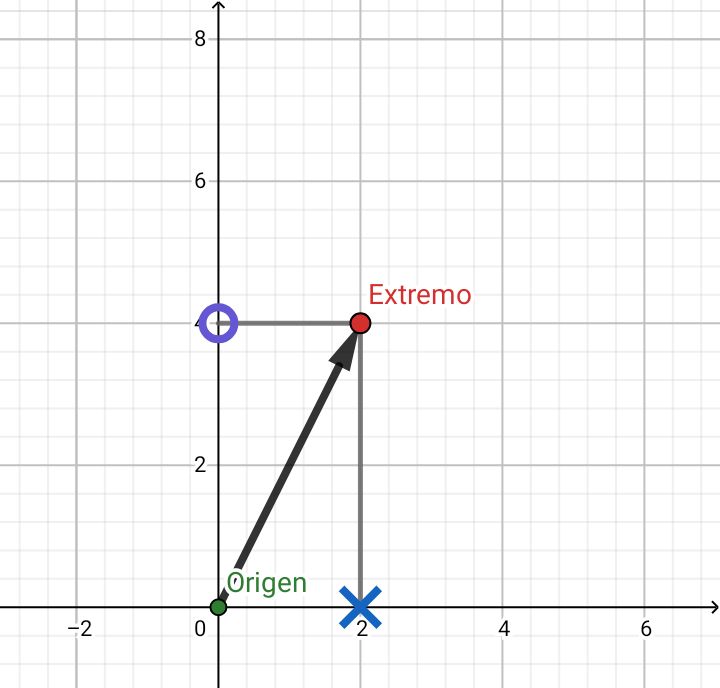
la X es el eje X
La O es el eje Y

Componentes de los vectores:

Los vectores tienen:

Módulo: Distancia entre el origen y el extremo.
Dirección: Linea donde el vector apunta.
Sentido: Puede tener una dirección, pero tener un sentido opuesto.

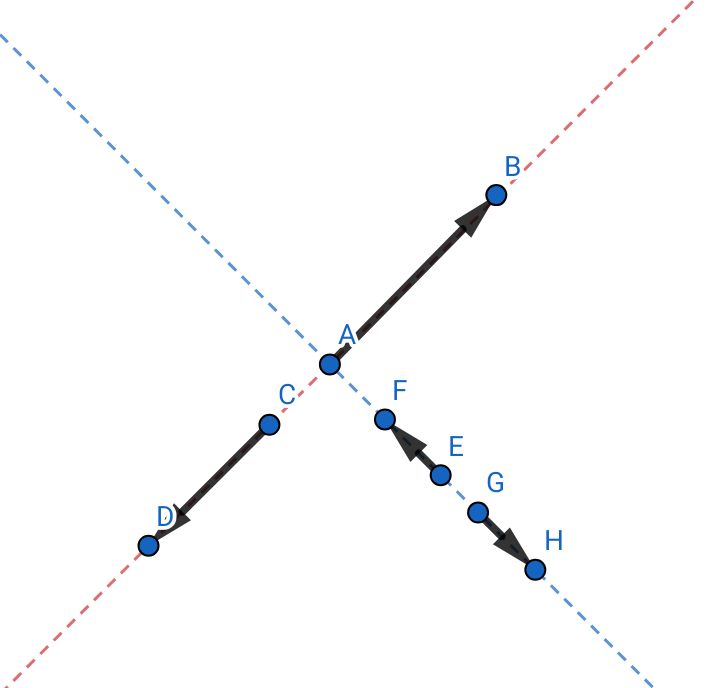
Las líneas de colores son las direcciones de los vectores que tienen encima, cada dirección tiene 2 vectores, están en sentido opuesto.

Los vectores de la línea azul tienen menor módulo que los de la línea roja, los de la línea azul son más pequeños, y más chibi.

Suma y multiplicación.

Los  vectores pueden sumarse y multiplicarse.

Suma:  Cuando hablamos de números (Llamados escalares en el álgebra de vectores) , cuando recorres 2 pasos, y después otros 2, recorres 4 desde tu lugar de inicio.

En las sumas vectoriales no es así siempre:

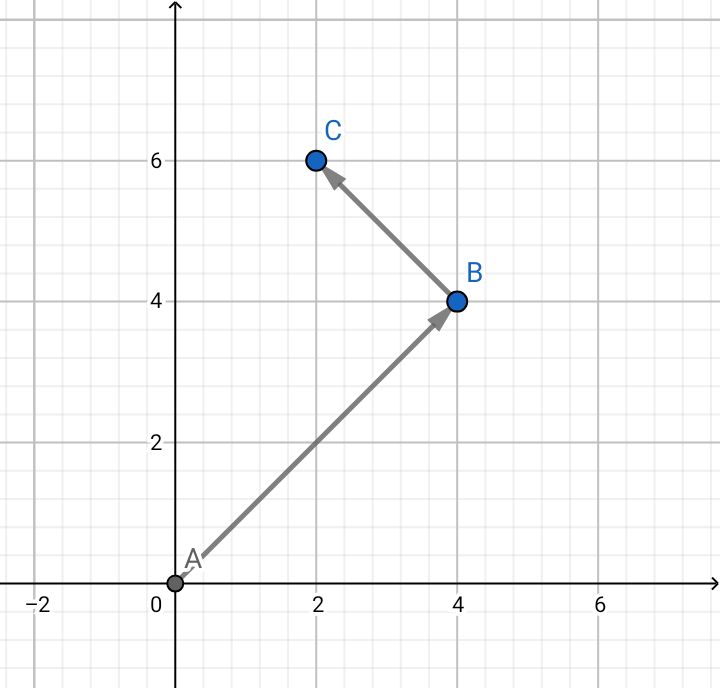
El primer vector sumado el segundo tiene un resultado diferente a la distancia total recorrida, la zona donde terminas no es la suma de los módulos, sino que es una diagonal.

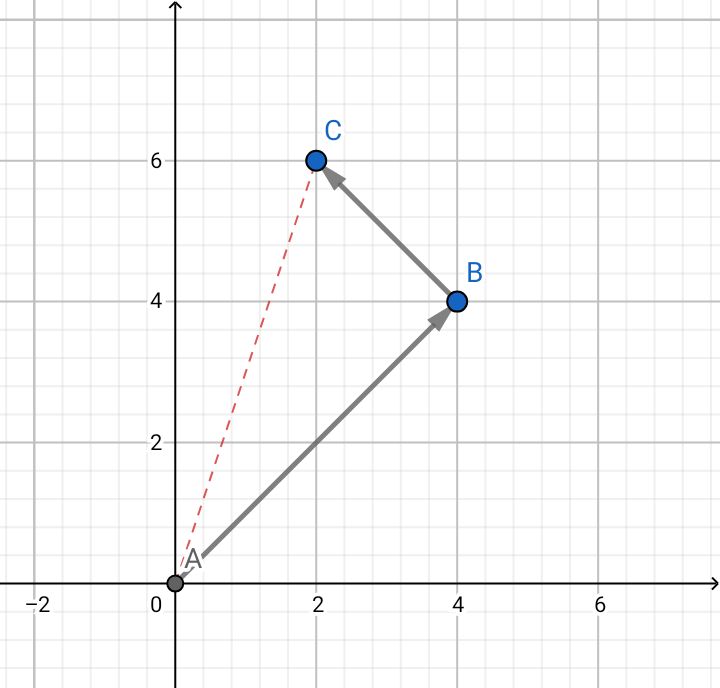
para sumar vectores debes hacer lo siguiente:

v = {2 ; 5}
u = {3 ; 4}

u+v = {2+3 ; 5+4}

y cuando se restan sólo se suma el opuesto:,
u + (-v)

Multiplicación:

Para multiplicar un vector se debe multiplicar el lado x de los vectores, y sumar por la multiplicación del lado y

v*u = (2*3+5*4)

o se multiplica ambos módulos junto a sus ángulos.

Módulo

para sacar el módulo de un vector se debe hacer el teorema de Pitágoras:

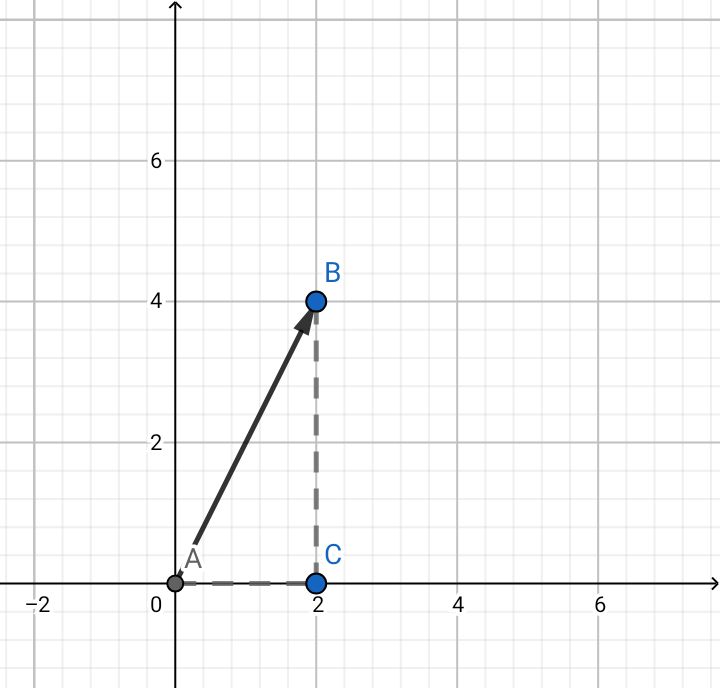
Vector:
v = {2 ; 4}

módulo:
|v| = √(2²+4²)