1) Introduction

Un repère est une structures géométrie définie par deux directions (souvent appelées Axes).
Ces directions donnent un sens à notre repère grâce à des vecteurs "unitaires", souvent appelée I et J.
Nous verrons plus tard l'utilité d'un repère.

Il existe plusieurs types de repères, que ce soit en deux dimensions (deux axes orientent le repère) ou en trois dimensions (trois axes orientent de repères).

2) Repères en Deux Dimensions

Définition :
Nous étudierons pour l'instant des repères en deux dimensions. Il y a deux façons de nommer un repère en deux dimension.

Propriétés :

- Un repère Orthogonal :

Cela signifie que les deux vecteurs qui orientent le plans sont perpendiculaire (on dit qu'il sont orthogonaux).

- Un repère Orthonormé :

Cela signifie que les deux vecteurs sont gradués de façon égale : à chaque case on augmente ou diminue de 1 peut importe la direction. On dit que les vecteurs on la même norme => orthonormé.

Remarque :
Un repère peut être à la fois orthogonal et orthonormé, soit l'un, soit l'autre ou ni l'un ni l'autre.

Exemple :

- Repère orthogonal et orthonormé, dit Orthonormal :

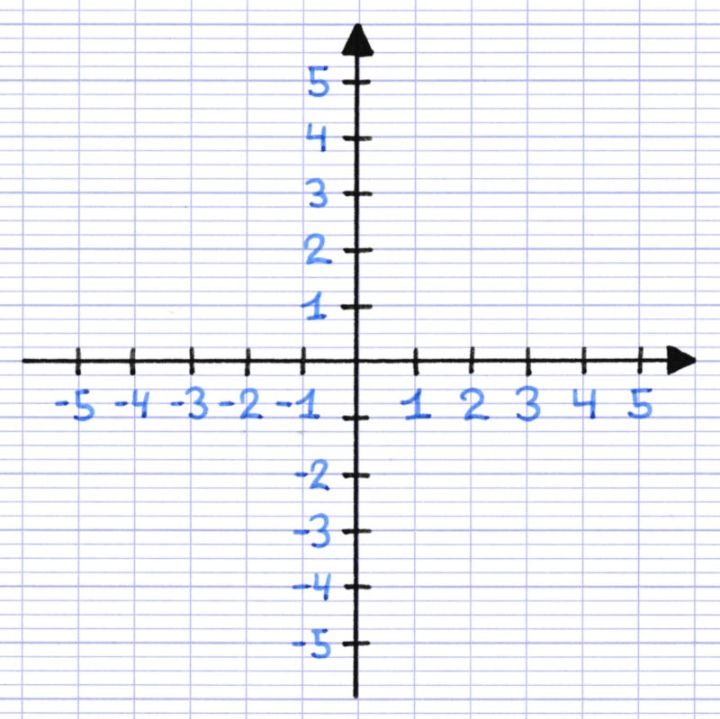
Les deux vecteurs direction sont "perpendiculaire" (dit orthogonal), et sont normé de la même manière.

- Repère orthogonal non-orthonormé :

Les vecteurs sont "perpendiculaire" (dit orthogonal), mais les vecteurs ne sont pas numéroté de la même manière : l'axe vertical et numéroté toutes les deux cases, l'axe horizontal est numéroté toutes les cases.

- Repère non-orthogonal et orthonormé :

Les deux vecteurs ne sont pas "perpendiculaire" (dit non-orthogonal), cependant ils sont normé de la même manière : une case correspond à une augmentation ou diminution de 1.
(Ne pas prendre en compte les cercles ni la diagonal sur le schéma)

- Repère non-orthogonal et non-orthonormé, dit Quelconque :

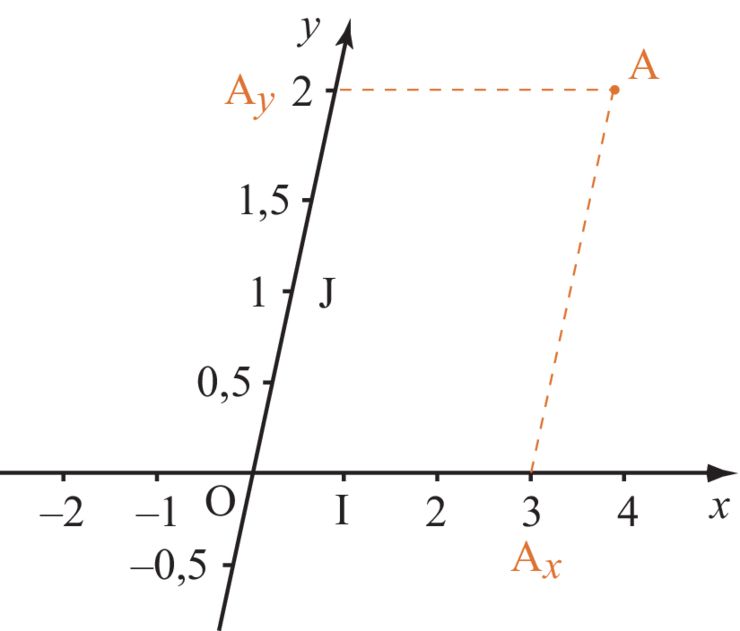
Les deux vecteurs directement sont ni "perpendiculaire" (dit non-orthogonal), ni numéroté de la même manière : vertical de 0,5 en 0,5 et horizontal de 1 en 1.
(Ne pas prendre en compte le point A en compte)

Récapitulatif :
Tous les repères vus précédemment sont en deux dimension. Ainsi :
Repères
- orthogonal non-orthonormé =
Orthogonal
- orthogonal orthonormé =
Orthonormal
- non-orthogonal orthonormé = Quelconque orthonormé
- non-orthogonal non-orthonormé = Quelconque

Remarque :
Généralement quand on parle d'un repère orthonormé, on suppose qu'il est orthogonal.

3) Les Axes en 2D

Définition 1 :
Les directions d'un repère sont définie par deux vecteurs nommés vecteur unitaires, ces vecteurs partent du centre du repère appelé O et on pour longueur 1 carreau.

Définition 2 :
En deux dimensions, les axes ont un noms spécifiques :
Axe horizontal x : abscisses
Axe vertical y : ordonnées
On verra que dans le cas des fonctions, l'axe y est "l'image" de l'axe x.

4) Repères en trois dimensions (compliqué)

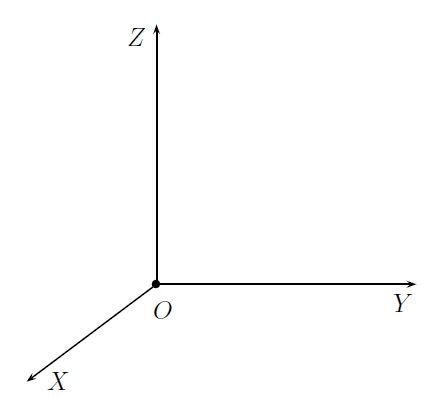
On voit qu'il y a bien 3 directions, contrairement au modèle en deux dimensions qui en possèdent seulement 2.

Propriétés :
Les propriétés des repères en deux dimensions s'appliquent pour celles en trois dimensions

Définition :
Dans le cas d'un repère en trois dimension, les axes sont définis en fonction de leur orientation.
Ici :
X = abscisses
Y = ordonné
Z = côte (toujours orienté verticalement)