Now that we have properly established what a function is, we can move onto investigating the derivative.
The derivative, simply put, is the function of the gradient of the function. That might be hard to understand for now but by the end of this chapter you should have a clear understanding of what it is.

At any point on a function, a tangent can be drawn. The tangent is a straight line that just touches the function at one point. In other words, the equation of the tangent, and the equation of the function, share a common point (or points, if the tangent intersects the line at another point).

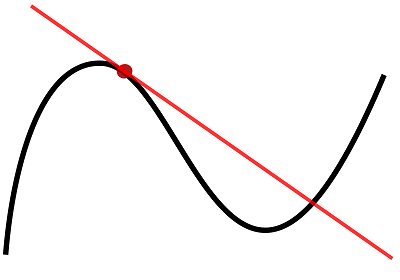
Here, we can see that the red line is the tangent whilst the black line is the function. The tangent touches the function at one point, and intersects it at another. Tangents always have to touch the function at one point, but doesn't necessarily have to intersect it at another point, even though it can.

Differential Calculus is used to find the gradient of the tangent, given a point on a function. To do this, the function is 'differentiated' to find its 'derivative'. The derivative is an equation, or in other words a formula,  that defines the gradient of the tangent on the function at any given point.

Here, the equation of the function,  y = x² + 1 has been graphed in red.
Substituting x = 1 into the equation shows us that y = 2.
Therefore the point (1,2) exists on this function.
The tangent at the point where x = 1 has been shown in blue. It touches the function at the point where x = 1, which means that it touches the function at (1,2).

Now by looking at the graph, we can deduce that the gradient of the tangent is 2 since
The gradient is equal to rise over run and the tangent slopes to the right.

But we are just lucky that this specific tangent has an easy gradient to calculate. What is a sure way to find the gradient of the tangent to a function given any point?

This is where the derivative comes in. The derivative will give you the gradient of the tangent at any x - value. Each function, any function, has a derivative. To find the derivative you have to differentiate the function. The method and proof for this will be shown later.

The derivative of a function is denoted by f'(x) (Pronounced; F-dash-x). There are other notations for the derivative but for now, this is the definition we will use.
The derivative of the parabola shown above, created by the function f(x) = x² + 1 is
f'(x) = 2x
(We will prove this later)

Using the derivative, f'(x) = 2x, we can find any gradient of any tangent on this function.
Let's use the example we have analysed above, where the tangent is at x = 1.

                                                                              f'(x) = 2(1)
                                                                              f'(x) = 2

Therefore the gradient of the tangent at the point where x = 1, is 2.
Let's say that we want to find the gradient of the tangent when x = 7

                                                                             f'(x) = 2(7)
                                                                             f'(x) = 14

Thus, the gradient of the tangent at the point where x = 7 is 14.

This works with any x - value, whether it be negative, positive, rational, irrational, fractional, or integer.
For example, the gradient of the tangent when x = -√2

                                                                             f'(x) = 2(-√2)
                                                                             f'(x) = -2√2

So the gradient of the tangent when x is -√2 is -2√2. It is negative so it slopes down.

As mentioned already, every function has a derivative, in this case, the derivative was f'(x) = 2x
The derivative can be long and complex, short and simple, but every function has one.
The derivative defines every possible gradient of the function.
In the next chapter, we will take a look at the First Principles, and the proof of the derivative.