Before we explore the differentiation of different functions, other notations for the derivative need to be introduced. 

So far, the notation we have used for the derivative has been f'(x) but you can also use dy/dx (pronounced dee why dee ecks) and y' (pronounced y - dash).

The notation for the derivative being f'(x) is what we have been using so far, and is called "Lagrange's notation".

The notation dy/dx you see on the cover of this guide is called "Leibniz's notation". It can be explained as being the notation for the limit of a fraction. Before, we defined the gradient between two points as "change in y over change in x". This is a fraction, and therefore, we can express this as:

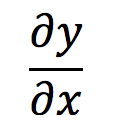
The weird "d" you see means "change in". As explored in First Principles, if we take the limit of this fraction, as change in x (remember our h?) approaches 0, we get the derivative. This is expressed as:

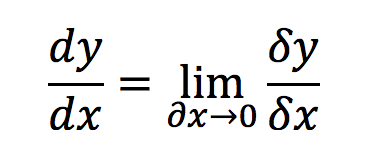
Therefore dy/dx is another notation for the derivative.

Since y is usually made the subject of the equation we are differentiating, we can replace it with the equation itself. For example, let's use the equation from previous chapters:

y = x²+1

Since y is equal to x²+1, we can replace the y in dy/dx giving us 

d(x²+1)/dx

The x²+1 can be taken out of the fraction, giving us:

This form is usually used when an equation is not defined. If the question only asks you to differentiate x²+1, as opposed to y=x²+1, the form above is usually used to denote the derivative.

Our final notation, y' is relatively easier to explain. We already know that f'(x) is used to represent the derivative when our function is given by f(x). 

y' comes in when our function is given by y. Remember that f(x) defines the function and y = f(x) defines the equation of the function. In the case that you are finding the derivative of an equation, you can use this as a notation for the derivative.

Throughout this guide, all of these notations will be used interchangeably. Remember that, they all represent the same idea; the derivative.

The next chapter will be all about differentiating the polynomial function.