Calculus concerns two main processes. Differentiation and Integration.

Differentiation is the examination of the gradient of a function at certain points, and as we have already seen, this must be done using the derivative of the function.
Integration is finding the area bounded by a function. (This guide only concerns differentiation)|

During the 17th Century, Sir Isaac Newton in England and Gottfried Leibniz in Germany had independently formalized the method of calculus. Their methods were based on the discovery that differentiation and integration were closely related. This became the 'Fundamental Theorem of Calculus'.

To properly introduce differential calculus and to properly prove how the derivative is found, we must understand the First Principles.

First Principles defines the derivative as a limit. Usually, we imagine that the gradient of a line can only be found if we know two points right? Well then, if the tangent only touches the function at one point, how do we know its gradient?

This is where the limiting process comes in. Two points are actually used to find the gradient of a tangent. The limiting process diminishes the distance between these two points so that it becomes one point. Using this method, the gradient of the tangent at the point can be found.

Let's take a look at the equation of the general function,  f(x). The equation y=f(x) creates the line on the graph.

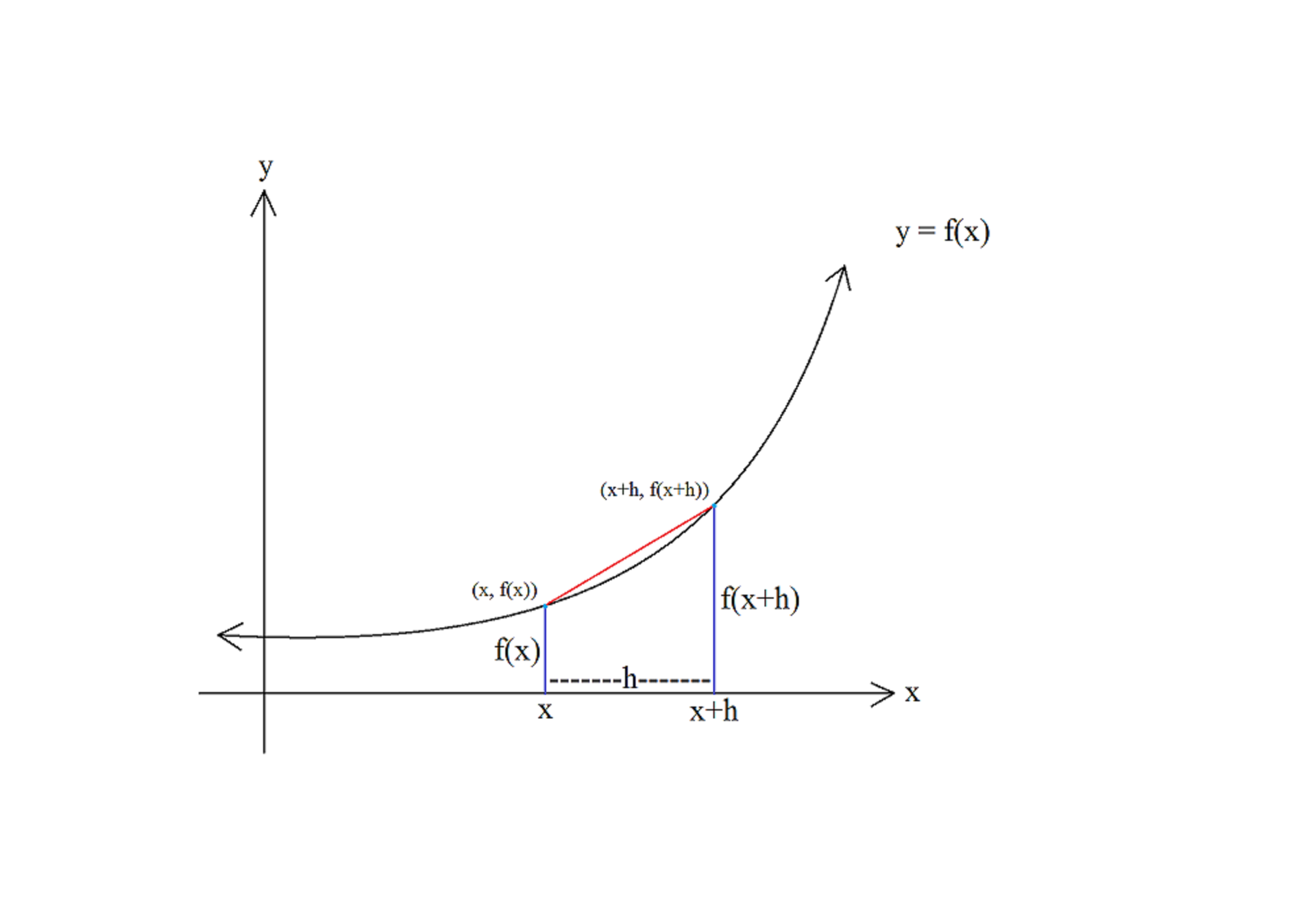
Our goal is to find the gradient at the point (x, f(x)).
On the x-axis, there is a point labeled x, and another point, which has a distance of 'h' units away. Thus this other point is labeled x + h.
The vertical distance from the x-axis to the line would be the y value.

Since y = f(x), the vertical distance from x to the line is f(x). The same applies to x + h, its vertical distance to the line being f(x+h).

Now we have two points, and that means we can find the gradient of the line between the two points (in red). Recalling from basic linear equations, the gradient of a line is equal to the rise over the run. Rise being changed in the y - value, whilst run being the change in the x - value.

In this case, our rise is given by f(x+h) - f(x) and our run, is given by h.
Therefore, our gradient of the red line is given by,

But this is the gradient of a line created by two points. How do you find the gradient of a tangent at one point?
Well, if you decrease the distance of x + h and you make it get infinitely closer to x, you end up with one point right? That one point being at x.
How do you do this? You decrease the value of h, to make the distance smaller. In fact, you decrease the value of h until it becomes zero. Thus we take the limit of h as it approaches 0, and when we do so, we finally get the derivative.
(Remember that the derivative is the equation that tells you the gradient of a tangent at a point. For now, it is denoted as f'(x))

The equation here sums it up.

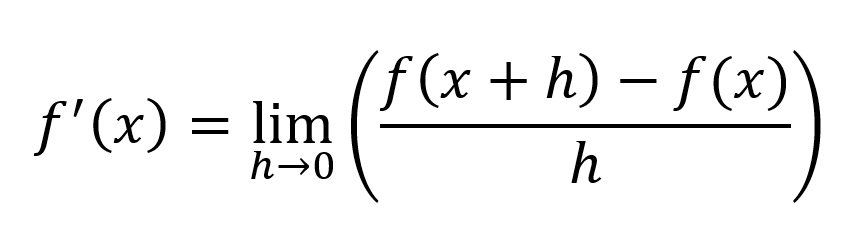
Remember our parabola from before?
We can now find its derivative properly, using First Principles.
From what we know, the function of the parabola was f(x) = x²+1.

Therefore, we use the limiting equation we have above, replacing f(x) with x²+1 since f(x) = x² + 1 is the function we are differentiating.

Expanding the numerator gives,

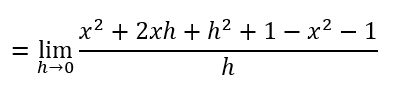
Then simplifying,

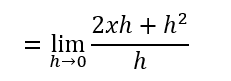
We can then factorize h from the numerator.

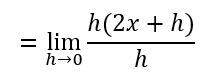
The h in the numerator and denominator divide and cancel out.
This gives,

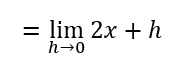
Since h approaches zero, we can now substitute h as 0 into the equation.
Once we do so, we prove the derivative of the function f(x) = x²+1.

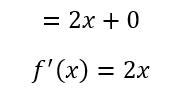
The derivative is 2x, and as shown in the previous chapter, this can be used to find the gradient of a tangent at any point.

Now we can see that by using First Principles and the limiting process, we can find the derivative of a function. In fact, you can use this on f(x) = 5x + 8, f(x) = 3x²-2x+18 or f(x) = 6x³, or virtually any polynomial function. The expanding and algebra can get very complicated though, especially with polynomials with higher powers.

That is why, from First Principles, we derive simpler formulas for differentiating all sorts of functions.

The First Principles are the fundamentals of differential calculus. From First Principles, we can derive simpler formulas for differentiating polynomial functions such as f(x) = x² + 1, and later on, it will show us how to differentiate trigonometric, logarithmic, and exponential functions.

In the next two chapters, we will take a look at the other notations for the derivative and introduce the general formula for finding the derivative of polynomial functions in a more efficient manner.