To differentiate polynomial functions we need to learn how to differentiate powers of x.
Whether the polynomial is,
y = x
y = 3x +8
y = 5x³-2x²+9x-15
it can be all easily differentiated using the formula that we will now prove, using First Principles. This formula will also come in handy when dealing with functions where something is to the power of another.

One property of differentiation is that, across operations such as addition, and subtraction, the derivative can be used separately on each term. 

In others words, lets say we were differentiating x²+1. Since the terms x² and 1 are separated by addition, the derivative of x² plus the derivative of 1 will be equal to the derivative of x²+1 altogether. This can be shown by:

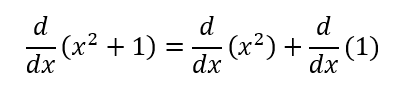
Remember, this only applies to addition and subtraction. This does not apply to multiplication and division. The methods for the differentiation of multiplication and division will be explored later.

The proof below requires knowledge of the binomial expansions. It is only used to prove this formula for differentiating powers of x and is not important in later stages of this guide.

To differentiate different powers of x, we need to first devise a general form for indices.
Let's say this "power" of x is n. Therefore we have:

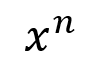
Putting this in an equation gives us:

Now, to differentiate, we use First Principles, using the same method from the chapter before.

By taking the limit of the change in x over change in y, we find the derivative.
'h' is used to denote change in x as always.

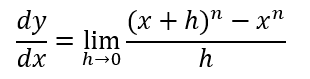
There is now the binomial expansion of x+h to the power n in the limit.

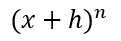
From binomial theorem and Pascal's triangle, we know that:

This expansion of the binomial gives us a finite series of terms, whose length is determined by the size of n, as shown above.
If we apply this to the binomial of 'x+h to the power of n', we get:

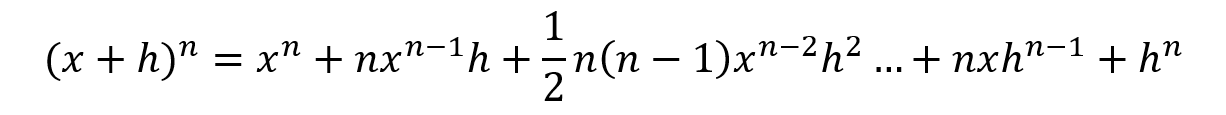
We can now rewrite our limit by replacing the binomial with its expansion.

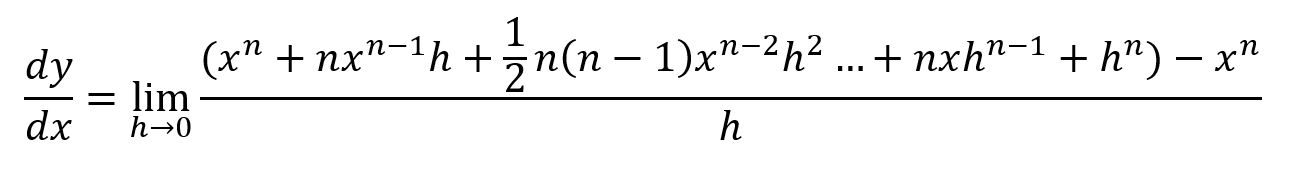
The positive 'x to the n', and the negative 'x to the n' on opposite sides in the numerator cancel each other out. We are left with:

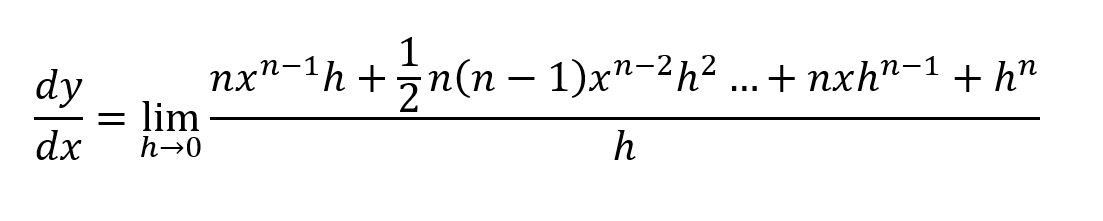
In the numerator, the 'h' is in every single term. Therefore, we can factorize h out of the numerator.

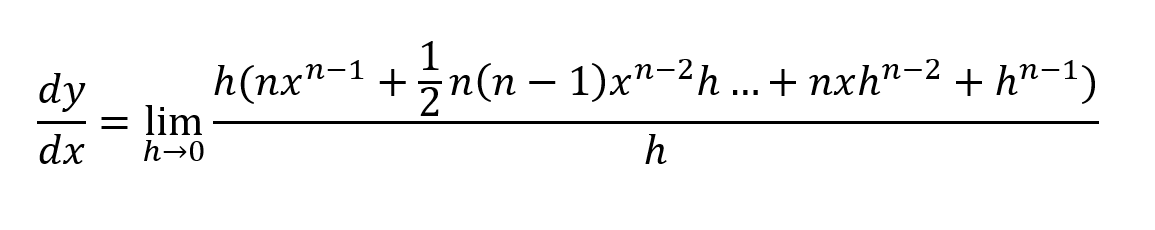
The h in the numerator and the h in the denominator divide, and cancel each other out. We are left with:

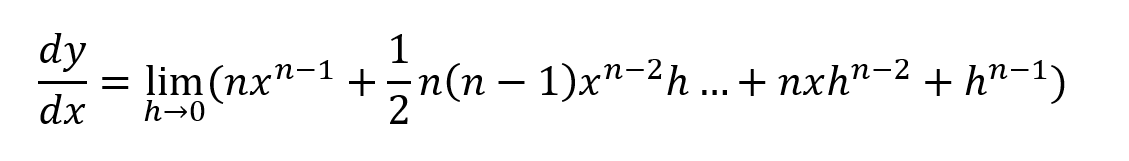
Every single term inside the limit is multiplied by h, except for the first. When we take the limit, h approaches 0, which means we can substitute h as 0. Since anything multiplied by 0 becomes 0, all the terms that are multiplied by h become 0 and disappear, leaving us with the first term.
Therefore:

Now, the formula for differentiating powers of x as been proven and derived using First Principles. As mentioned before, we can use this to find the derivative of any polynomial function.

This proof, however, requires knowledge of binomial expansions, which is quite advanced. An easier proof, which uses difference of two powers, will be added in the future.

Let's go back to our the equation y=x²+1

This can be rewritten as y=x²+x⁰ because anything to the power of 0 is 1.

To differentiate this, we can apply the formula we have just proved above:

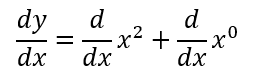
In the first term, n=2. In the second term, n=0. We then substitute these value into the formula we proved.

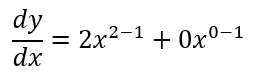
For the second term, anything multiplied by 0 is 0, so the whole term becomes 0. When we simplify the first term we get:

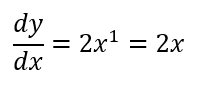
We have shown once again, that the derivative of y=x²+1 is 2x.

You can now see that the formula that we have proved in this chapter is very easy to use. Use this formula on any polynomial function, or equation as it is the fastest way to differentiate. In fact, this formula is always used in the process of differentiating functions containing something to the power of another.

Different rules need to be used when we are differentiating a function within another function, a function multiplied by another function or a function divided by another function.

In the next chapter, we will look at more examples where this formula can be used. Later on, we will investigate and prove these "other rules" for differentiating.